The epidemiologic concept of R naught (R0) is much in the news of late. This number, the basic reproduction number, is being used to calculate COVID-19 transmissibility and is a key part of the discussion on when to begin allowing cities and states to reopen.
What R Naught (R0) Means
R naught (R0), the basic reproduction number, is one of the most fundamental and often-used metrics for the study of the way a disease spreads. The symbol R represents the actual transmission rate of a disease and stands for reproduction. Naught, or zero, stands for the zeroth generation (patient zero). It refers to the first documented patient infected by a disease in an epidemic.
R0 is an indicator of the contagiousness or transmissibility of infectious and parasitic agents and represent the number of new infections estimated to stem from a single case in a population that has never seen the disease before. If the R0 is 2, then one person is expected to infect, on average, two new people (Anastassopoulou et al., 2020).
To provide some perspective, seasonal strains of flu have R0s between 0.9 and 2.1. The R0 value of the 1918 flu pandemic was estimated to be between 1.4 and 2.8, and for an extremely contagious disease such as the measles, R0 is thought to lie between 12 and 18 (Healthline, 2020).
R0 is one of the key values that can predict whether an infectious disease will spread into a population or die out. It is used to assess the severity of the outbreak, as well as the strength of the medical and/or behavioral interventions necessary for control (Breban et al., 2007).
Covid-19 R Naught
The R0 originally estimated for COVID-19 was between 2.2 and 2.7, but data collected from case reports across China reported a much higher R0. Results showed that the doubling time early in the epidemic in Wuhan was 2.3 to 3.3 days. From this data, researchers calculated a median R0 value of 5.7. This means that each person infected with the virus can transmit it to 5 to 6 people rather than only 2 to 3 as previously thought (Sanche et al, 2020).
How a Virus With a Reproduction Number (R0) of 2 Spreads
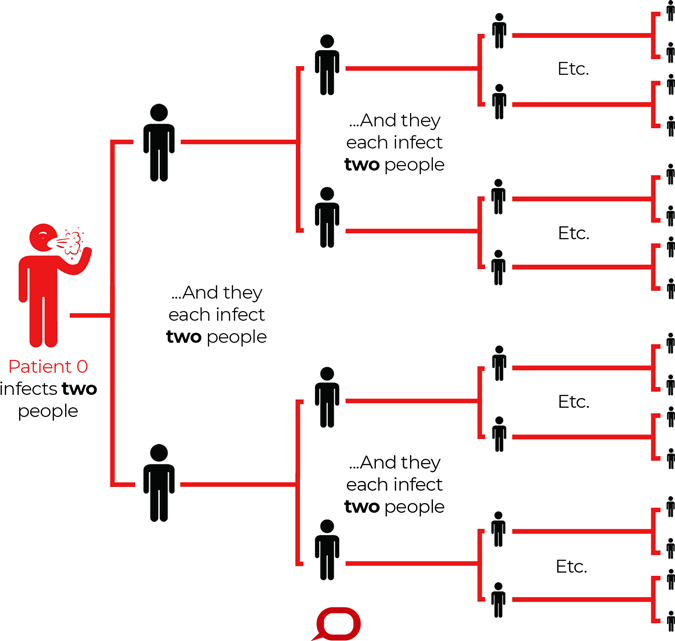
R0 describes how many cases of a disease an infected person will go on to cause—in this imagined scenario R0=2. Source: The Conversation, CC BY-ND.
History of R0
Mathematical demographer Alfred Lotka developed the Stable Population Theory during the early twentieth century to study the change and growth rate of certain populations. He proposed the reproduction number in the 1920s as a measure of the rate of reproduction in a given group of people and used it to count offspring.
In the 1950s, epidemiologist George MacDonald suggested using R0 to describe the transmission potential of malaria. He proposed that if R0 is less than 1, the disease will die out in a population, because on average an infectious person will transmit to fewer than 1 other susceptible person. On the other hand, if R0 is greater than 1, the disease will spread (Eisenberg, 2020). Since then the reproduction number has become widely used in the field of epidemiology.
How R0 is Used
R0 values indicate if a disease will spread or decline within a community and how far and how rapidly transmission will occur. It can also inform public health policy decisions used to mitigate spread.
The higher the R0, the more likely the disease will become an epidemic. There are three different possibilities that can be conveyed by R0 (Healthline, 2020):
- If R0 is less than 1, the disease will not spread and will eventually die out.
- If R0 is 1, the disease will remain stable in the community but will not cause an epidemic.
- If R0 is greater than 1, the disease will spread and may cause an epidemic.
How R0 is Calculated
R0 is determined using complex mathematical equations that look at data from the disease’s characteristics and transmissibility, human behavior, how often sick and susceptible people are expected to come into contact with each other, and where the affected community is located. Scientists may also add educated guesses.
One of the ways epidemiologists calculate R0 is by using contact tracing data obtained at the onset of the epidemic. Once an individual is diagnosed, that person’s contacts are traced and tested. R0 is then computed by averaging the number of secondary cases caused by diagnosed individuals (Breban et al, 2007).
However, counting the number of cases of infection during an epidemic can be extremely difficult, even when public health officials use active surveillance and contact tracing to attempt to locate all infected persons. Although measuring the true R0 value is possible during an outbreak of a newly emerging disease, there are rarely sufficient data collection systems in place to capture the early stages of an outbreak when R0 might be measured most accurately (EID, 2019).
As a result, R0 is nearly always estimated retrospectively from sero-epidemiologic data (which looks for the presence of antibodies in the blood) or by using theoretical mathematical models. The estimated values of R0 generated by mathematical models are dependent on numerous decisions made by the modeler (EID, 2019).
When mathematical models are used, R0 values are often estimated by using ordinary differential equations, but high-quality data are rarely available for all components of the model. The population structure of the model includes people who are exposed but not yet infectious, as well as assumptions about demographics such as births, deaths, and migration over time (EID, 2019).
The Effect of Vaccination
When examining the effect of vaccination, the more appropriate term to use is the effective reproduction number (R), which is similar to R0 but does not assume complete susceptibility of the population and therefore can be estimated with populations having immune members (EID, 2019).
Efforts aimed at reducing the number of susceptible persons within a population through vaccination would result in a reduction of the R value, rather than R0 value. In this scenario, vaccination could potentially end an epidemic if R can be reduced to a value <1. The effective reproduction number can also be specified at a particular time t, presented as R(t) or Rt, which can be used to trace changes in R as the number of susceptible members in a population is reduced. When the goal is to measure the effectiveness of vaccination campaigns or other public health interventions, R0 is not necessarily the best metric (EID, 2019).
The potential size of an outbreak or epidemic is often based on the magnitude of its R0 value, and R0 can be used to estimate the proportion of the population that must be vaccinated to eliminate an infection from that population—the higher the R0, the more people must be vaccinated (EID, 2019).
Vaccination campaigns reduce the proportion of a population at risk for infection and are highly effective in mitigating future outbreaks. This conclusion is sometimes used to suggest that an aim of vaccination campaigns is to remove susceptible members of the population in order to reduce the R0 for the event to less than 1. Although the removal of susceptible members from the population will affect infection transmission by reducing the number of contacts between infectious and susceptible persons, it will technically not reduce the R0 value because the definition of R0 assumes a completely susceptible population (EID, 2019).
Cumulative Incidence Models
Another more commonly used approach is to obtain R0 from cumulative incidence data which is “the probability of developing disease over a stated period of time.” Theorists construct models based on Ordinary Differential Equations (ODEs) which describe the dynamics of the expected population size in different disease stages without tracking individuals. These types of modeling assumptions are hypothetical and cannot be verified using population-level data (Breban et al., 2007).
ODE models are formulated in terms of disease transmissibility and progression rates in the population, which yield a threshold parameter for an epidemic. The epidemic threshold is a boundary where disease equilibrium becomes unstable (R0 is greater than 1) and an epidemic may begin (Breban et al., 2007).
Calculations of R0 that use cumulative incidence data often use three primary parameters:
- The duration of contagiousness after a person becomes infected (how long the virus can be transmitted by an infected person). The longer someone is contagious, the higher the R0 is.
- The likelihood of infection per contact between a susceptible person and an infectious person or vector.
- The contact rate (the rate at which an infected person meets susceptible people).
Sometimes other parameters are added, such as the availability of public health resources, the policy environment, various aspects of the built environment, and other factors that might influence transmission.
R0 can also depend on viral characteristics, how it spreads and how long it can survive in the air and on objects. It also depends on where the virus is found in the world. According to Paul Delamater, from the University of North Carolina at Chapel Hill, “There’s a host of social, cultural, and demographic characteristics of places that would make the R naught value differ from place to place.” For any given infectious agent, the scientific literature might present numerous R0 values (EID, 2019).
Difficulties Calculating R0
Despite its place at the forefront of mathematical epidemiology, the concept of R0 has many flaws and defining it can be difficult. Few epidemics are ever observed at the precise moment an infected individual enters a susceptible population, so calculating the value of R0 for a specific disease relies on secondary methods (Li et al., 2016).
In the hands of experts, R0 can be a valuable concept. However, the process of defining, calculating, interpreting, and applying R0 is far from straightforward. The simplicity of an R0 value masks the complicated nature of this metric. Although R0 is a biologic reality, the interpretation of R0 estimates derived from different models requires an understanding of the models’ structures, inputs, and interactions. “Because many researchers using R0 have not been trained in sophisticated mathematical techniques, R0 is easily subject to misrepresentation, misinterpretation, and misapplication” (EID, 2019).
Even if the infectiousness of a pathogen and the duration of contagiousness are constant, R0 will fluctuate if the rate of human-to-human or human-to-vector interaction varies. Any factor that can influence the contact rate—including population density, social organization, and seasonality—will ultimately affect R0 (EID, 2019). Since a pandemic occurs across many different populations, geographies, and climates, the R0 may vary considerably from country to country or even within a country.
Because R0 is a function of the contact rate, the value of R0 is a function of human social behavior and organization, as well as the innate biologic characteristics of a pathogen. More than 20 different R0 values were reported for measles in a variety of study areas and periods, and a review in 2017 identified feasible measles R0 values of 3.7 to 203.3. This wide range highlights the potential variability in the value of R0 for an infectious disease dependent on local societal behavior and environmental circumstances (EID, 2019).
There are many diseases that can persist with R0<1, while diseases with R0>1 can die out, reducing the usefulness of the concept as a threshold for an epidemic. For example, it is possible that a disease can persist in a population when already present but would not be strong enough to invade. Also, the threshold value that is usually calculated is rarely the average number of secondary infections, diluting the usefulness of this concept even further (Li et al., 2011).
Many of the parameters included in the models used to estimate R0 are merely educated guesses; the true values are often unknown or difficult to impossible to measure directly. This limitation is compounded as models become more complex. So, although only one true R0 value exists for an infectious disease event occurring in a particular place at a particular time, models that have minor differences in structure and assumptions might produce different estimates of that value, even when using the same epidemiologic data (EID, 2019).
Public Health Measures That Decrease R0
When the R0 of a newly emerged disease indicates that an epidemic may occur, it is important to understand the processes that can limit transmission (R) of a disease in totally susceptible people in order to prevent epidemics from starting (or to limit their size). Once a country realizes that a new virus exists, measures must be taken to interrupt the chain of infection until treatments and vaccines can be developed.
Measures used successfully in previous epidemics, which have been shown to reduce the R0 of a disease are:
- Screening
- Social distancing
- Tracking and tracing of exposed people and their contacts
- Handwashing
- Masking
- Quarantining
- Providing healthcare workers with proper protective equipment
- Vaccination
Superspreading Events
Although we still have much to learn about the epidemiology of coronavirus disease, there have been multiple reports of superspreading events. During recent severe outbreaks of SARS, Middle East respiratory syndrome (MERS), and Ebola virus disease, superspreading events were associated with explosive growth early in an outbreak and sustained transmission in later stages (Frieden & Lee, 2020, June).
Superspreading events highlight a major limitation of the concept of R0. The basic reproductive number R0, when presented as a mean or median value, does not capture the heterogeneity of transmission among infected persons; two pathogens with identical R0 estimates may have markedly different patterns of transmission. The goal of a public health response is to drive the reproductive number to a value <1, something that might not be possible in some situations without better prevention, recognition, and response to superspreading events. A meta-analysis estimated that the initial median R0 for COVID-19 is 2.79 (meaning that 1 infected person will on average infect 2.79 others), although current estimates may differ because of insufficient data (Frieden & Lee, 2020, June).
Countermeasures can substantially reduce the reproductive number; on the Diamond Princess cruise ship, an initial estimated R0 of 14.8 (~4 times higher than the R0 in the epicenter of the outbreak in Wuhan, China) was reduced to an estimated effective reproductive number of 1.78 after on-board isolation and quarantine measures were implemented (Frieden & Lee, 2020, June).
In Wuhan, aggressive implementation of nonpharmaceutical interventions in the community, including a cordon sanitaire* of the city; suspension of public transport, school, and most work; and cancellation of all public events reduced the reproductive number from 3.86 to 0.32 over a 5-week period. However, these interventions might not be sustainable (Frieden & Lee, 2020, June).
*Cordon sanitaire: a quarantined geographic area, guarded to prevent the movement of people in or out of the area.
Although superspreading events appear to be difficult to predict and therefore difficult to prevent, understanding the pathogen, host, environmental, and behavioral drivers of superspreading events can inform strategies for prevention and control. This includes:
- Pathogen-specific factors
- Binding sites
- Environmental persistence
- Virulence
- Infectious dose
- Host factors
- Duration of infection (prolonged carriage)
- Location and burden of infection (e.g., laryngeal or cavitary tuberculosis)
- Symptomatology
- Environmental factors
- Population density
- Availability and use of infection prevention and control measures in healthcare facilities
- Behavioral factors
- Cough hygiene
- Social customs
- Health-seeking behavior
- Adherence to public health guidance
- Response factors
- Timely and effective implementation of prevention and control measures within the community and in healthcare settings
- Rapid identification and isolation of cases
- Effective case isolation and contact tracing (Frieden & Lee, 2020, June)
